磨課,是集各位老師的備課、授課精華,集自己平時積累的教學經驗反複推敲、反複講解的過程。磨課的特點是:同課異構,各位專家老師給出教學診斷。 一個“磨”字道出了其中的反反複複、斟酌修改和耗費的大量汗水!一個“磨”字,猶如俠客十年磨一劍、修煉得道一樣,道出了一節成功好課的艱辛和不易!
線性代數是理工科重要的基礎課程,課程教學涉及的人數多。與其他基礎課程相比,這門課程概念多,内容相對複雜,研究對象也更為抽象。學生學習起來容易入門但是深入較難,這讓同學們在學習線性代數的過程中容易産生畏難情緒甚至半途放棄。因此,在教學中适時的激勵學生、調動他們對《線性代數》課程學習的興趣,是幫助同學們順利完成該課程學習的關鍵。我認為:适時的介紹數學家刻苦努力、進取創新的精神,融數學發展史、數學文化史、課程思政教育于線性代數課堂教學可有利的促進線性代數課程的教學。具體而言,實際教學可以從以下幾個方面來打磨:
1. 課程教學引入生活案例,擯棄數學無用論
一些學生在高中階段疲于解題技巧的訓練,步入大學階段接觸的數學課程又是抽象難懂,所以對數學類課程内心存有畏難情緒,心裡暗示作用凸顯。另外,因為大學階段數學類課程都開設在大一、大二階段,他們暫時未接觸過相關專業課程,無法建立數學課程與其他專業課程的聯系,認為這類課程并不實用,提不起學習的興趣。
行列式和矩陣是初學線性代數這門課程的重點和難點,也是學習這門課程的起點。在講解二階、三階行列式時,如果引入三階行列式:
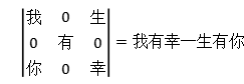
這個行列式稱為愛情行列式。
我想通過講解這個行列式,同學們會對行列式的學習充滿好奇,同時也能清楚地認識到行列式在生活中無處不在,從而提高學習《線性代數》課程的興趣。
現代社會,特别是大學生格外講究美,注重飲食健康問題。因此減肥也就成了很多年輕人喜歡探讨的問題。衆所周知每一種食物都有它的營養素含量,比如:卡路裡、蛋白質、碳水化合物等含量,我們可以根據營養素利用矩陣建立健康飲食的模型,這個模型簡單易建,容易理解,同學們也會比較感興趣并增加學習積極性。
國家建設涉及到工業、農業、國防、科技等各個領域,而每一個領域都有不同的層面,據此,我們也可以利用矩陣建立模型。同學們會感到今天的學習與祖國的建設密切相關,從而增強學習的動力、增強主人公的感覺。
2. 融數學史于課堂教學,培養學生們的科學精神,激發愛國情懷
行列式、矩陣、向量是線性代數中三個基本的計算單元。線性代數教學一般利用高斯消元法解線性方程組而引入行列式的概念及應用。我們可以引導學生們回顧數學史,以加深對這些内容的理解。告訴同學們有史書記載,行列式是由萊布尼茨和日本數學家關孝和發明的,而後克萊姆在其著作《線性代數分析導論》中對行列式進行了系統的闡述,并給出了利用行列式解線性方程組的方法——克萊姆法則。 我國東漢初年成書的《九章算術》中記載有求解線性方程組的方法,其計算步驟中的偏乘、直除就類似于今天初等變換的倍法變換和消法變換。告誡同學們,前輩們發明創造的知識今天我們來學習,沒有理由不學好、學不好!
3. 将數學文化引入教學課堂,培養科學審美能力、提高同學們的美學修養
數學家伽利略說:“自然這部巨著是用數學語言寫成的”。數學不僅是一種學術形态,還是一種文化,它用自己特有的語言和符号解釋着自然界的規律。線性代數的内在美體現在簡潔、規範;外在美體現在應用性強,便于操作。
同樣以行列式為例,行列式是線性方程組求解過程中提出的一種速記表達式。n階行列式的定義是
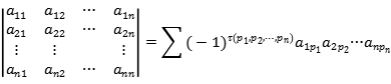
這個表達式抽象難記,我們可以這樣引導:
n階行列式的展開式中每一乘積項都來自于不同的行和不同的列,即從行來看,每一行都有且僅有一個元素被取到,從列來看,每一列也都有且僅有一個元素被取到,這體現了均衡性美;再深入引導,對角行列式的定義是對角線上元素不全為0,其他元素全為0,這從形式上來看,對角行列式特點就是關于主對角線對稱,它體現了一種對稱美; 計算高階行列式常用方法的是化一般行列式為三角形行列式再計算,實質是一個化繁為簡的過程,這體現了簡潔之美。矩陣是線性代數的核心内容,矩陣是将元素排成行、列的數表,有了這個概念,元素不再顯得雜亂無章,這體現了線性代數的整潔之美。在n階方陣裡還有一類行列式不等于0的方陣稱為奇異矩陣,這是矩陣的奇異之美。通過這樣的講解應該說把枯燥難學的數學内容和事物的美學聯系了起來,會極大的調動同學們的學習興趣和積極性。
作為一名高校教師,在課堂上為同學們講好課、講精品課是天職。為了講好課,課前進行必不可少的課程研讀和精心打磨,是教書育人、對學生負責的具體體現。怎樣上好《線性代數》這門課?怎樣融思政教育于《線性代數》課程教學?怎樣激發同學們的學習積極性、發揮同學們的主觀能動性,提高知識的應用能力?怎樣培養同學們的科學審美能力,樹立正确的人生觀、世界觀、價值觀值得我們認真推敲,打磨。




